How much Power is in the wind?

How much energy content is in the wind and how much power a wind turbine can generate from a given wind speed can be explained by the following formula


So, the power generated by a wind turbine depends upon air density, rotor disc area, and wind speed. Usually, we consider air density as constant thus only rotor area and wind speed mostly determine the wind turbine power.
Rotor Disc Area
The rotor disc area is the area over which the wind turbine sweeps. Thus, wind turbines can harvest from the entire area with relatively little blade area
The bigger the size of a wind turbine rotor, the more energy the wind turbine blade can harvest from the available rotor disc area.

Since the rotor disc area increases with the square of the rotor diameter, so doubling the size of the rotor increases the available energy four times.
Wind Speed
There is a cubic relation between power and wind speed as can be seen from the above power formula.
This means that if we double the wind speed, the power increase would be by a factor of 8. So considering this, Wind speed is the most critical factor that affects the power generated by wind turbines.
Wind Power Formula Derivation
How above wind power formula has come up? Let us derive that.
Consider a cylindrical volume of air flowing through a window of area, A[m2], with length, L[m], and air velocity, V [m s-1]. The mass of the air in this volume, m, can be found by m = L rho A with the density of air, (rho), taken to be 1.2 kg/m3.

The kinetic energy in the volume of air is found by

and the power P[watt] is expressed as

with t[s] being the time it takes to move the volume through the window and can be expressed as

Thus putting kinetic energy and time expression into the power formula we get


This is the derived formula that we have used in the above analysis.
If we divide the power P by cross-sectional area A, we get the term power density which is

The power density unit is w/m2 and for a wind speed of 10 ms-1 we get the power density as
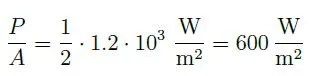
and for v=20 ms-1 we get almost 5 kW/m2. But remember that, we can’t extract this all due to the Betz limit.

